L’utilisation de la moyenne mobile sur les marchés date depuis la deuxième guerre. C’est un des premiers indicateurs le plus utilisé dans le domaine de l’analyse technique. L’objectif est de lisser les cours de clôture sur une période, d’indiquer la tendance des cours, soit à la hausse ou à la baisse.
Les moyennes mobiles jouent aussi le rôle de support et de résistance. Elles sont un indicateur de sur-achat, lorsque les cours s’éloignent trop au-dessus de leur moyenne dans une tendance haussière ou sur vendu ; c’est pareil lorsque les cours s’éloignent trop au-dessous de leur moyenne dans une tendance baissière.
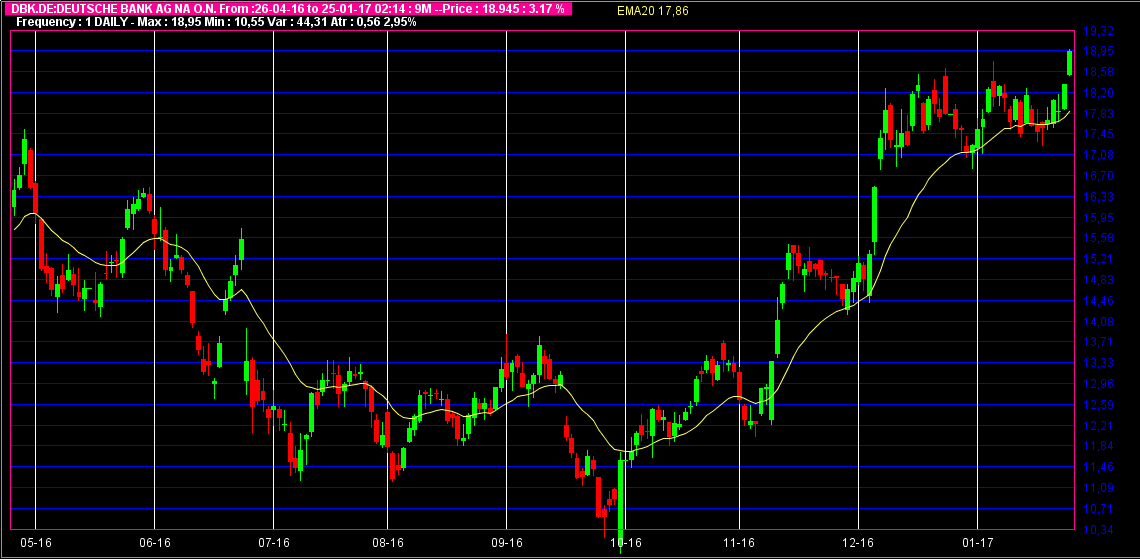
La figure-1 montre un exemple de moyenne mobile sur le graphique journalier de la Deuche Bank. On voit bien que la courbe de la moyenne mobile en jaune est plus lisse que celle des cours qui sont chandelier japonais.
Il existe plusieurs types de moyenne mobile ma
is les deux les plus utilisées sont : la moyenne mobile simple ou Simple Moving Average (SMA) et la moyenne mobile exponentielle ou Exponential Moving Average (EMA). Dans les moins utilisés, il existe la moyenne mobile déplacé Deplaced Moving Average (DMA), Weighted Moving Average (WMA), etc.
Moyenne mobile simple ou Simple Moving Average (SMA)
La moyenne mobile simple est calculée en additionnant les derniers cours de clôtures sur une période et en divisant cette somme par cette période. Une moyenne mobile de 5 jours représente le prix moyen sur les derniers 5 jours, celle de 20 jours représente le prix moyen sur les derniers 20 jours.
Moyenne Mobile Simple = (P1 + P2 + …Pn) ÷ N
P : est le Prix
N: est le nombre de Bars
Le tableau suivant présente un exemple de calcul d’une moyenne mobile simple de 5 sur les cours de clôtures journaliers de l’indic
e NASDAQ :
- Au 07/12/2015 faire la somme des derniers 5 cours de clôtures : 5156,31 + 5123,22 + 5037,53 + 5142,27 + 5101,81 = 25561,14
- Puis diviser la somme par 5 : 25561,14 / 5 = 5112,23 est la moyenne mobile simple
- Au 08/12/2015 pareil faire la somme des dernier 5 cours de clôtures : 5123,22 + 5037,53 + 5142,27 + 5101,81 + 5 045,73 = 25503,07.
- Puis diviser la somme par 5 : 25503,07/ 5 = 5100,61 est la moyenne mobile simple
- La différence entre le premier calcul et le deuxième c’est tout simplement le premier cours du 01/12/2015 qui a été remplacé par le dernier cours au 08/12/2015
- Ainsi de suite
| Date | Open | High | Low | Close | RowId | SMA(5) |
|---|---|---|---|---|---|---|
| 01/12/2015 | 5 129,64 | 5 156,31 | 5 120,17 | 5 156,31 | 1 | |
| 02/12/2015 | 5 158,82 | 5 176,77 | 5 117,15 | 5 123,22 | 2 | |
| 03/12/2015 | 5 143,16 | 5 144,60 | 5 011,72 | 5 037,53 | 3 | |
| 04/12/2015 | 5 050,93 | 5 147,00 | 5 043,49 | 5 142,27 | 4 | |
| 07/12/2015 | 5 139,46 | 5 139,78 | 5 082,23 | 5 101,81 | 5 | 5112,23 |
| 08/12/2015 | 5 050,52 | 5 111,73 | 5 045,73 | 5 098,24 | 6 | 5100,61 |
| 09/12/2015 | 5 077,21 | 5 106,37 | 5 000,12 | 5 022,87 | 7 | 5080,54 |
| 10/12/2015 | 5 026,30 | 5 075,65 | 5 019,31 | 5 045,17 | 8 | 5082,07 |
| 11/12/2015 | 4 979,77 | 4 996,19 | 4 928,67 | 4 933,47 | 9 | 5040,31 |
| 14/12/2015 | 4 932,61 | 4 953,60 | 4 871,59 | 4 952,23 | 10 | 5010,40 |
Vous pouvez télécharger cet exemple en ficher Excel
Plus la période est longue plus la courbe de la moyenne mobile est lisse. Cependant, la moyenne mobile de 50 jours est plus lisse que celle de 20 jours et celle de 200 est encore plus lisse que celle de 50 jours. En d’autres termes, plus la période est longue moins la moyenne mobile réagit au mouvement des cours.
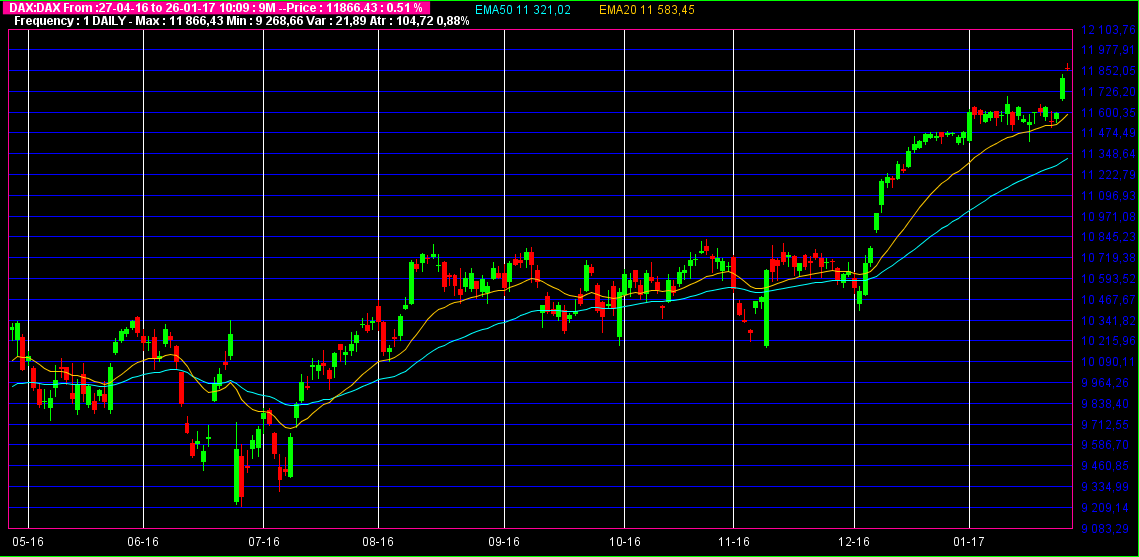
La figure-2 montre un exemple de trois moyennes mobiles simples de 20 jours, 50 jours et 200 jours. On peut constater que plus la durée est longue plus la courbe de la moyenne mobile est lisse et elle réagit mois vite au dernier cours.
Moyenne mobile exponentielle ou Exponential Mouving Average (EMA)
L’unique différence entre la moyenne mobile simple et la moyenne mobile exponentielle c’est que la moyenne mobile exponentielle réagir plus vite au dernier cours par rapport à la moyenne mobile simple.
Comme nous avons vu précédemment dans le calcul de la moyenne mobile simple tous les cours ont le même poids puisque on divise la somme par la période en revanche dans le calcul de la moyenne mobile exponentielle le cours le plus récent a plus de poids que le cours le mois récent et ainsi de suite jusqu’au premier cours qui a le plus faible poids
Le tableau suivant présente un exemple de calcul d’une moyenne mobile exponentielle de 5 sur les cours de clôtures journaliers de l’indice NASDAQ :
- Au début calculer le multiplicateur m = 2 / (1+periode) = 2 / (1+5) = 0,3333333
- Au 07/12/2015 faire le calcul d’une moyenne mobile simple (somme des derniers 5 cours de clôtures : 5156,31 + 5123,22 + 5037,53 + 5142,27 + 5101,81 = 25561,14 et diviser par 5) / 5 = 5112,23
- Au 08/12/2015 calculer
- multiplicateur x (cours de clôture – moyenne mobile exponentielle (précédente)) + moyenne mobile exponentielle (précédente)
- 3333333 x (5 098,24 – 5112,23) + 5112,23 = 5107,57
- Ainsi de suite
| Date | Open | High | Low | Close | RowId | EMA(5) |
|---|---|---|---|---|---|---|
| 01/12/2015 | 5 129.64 | 5 156.31 | 5 120.17 | 5 156.31 | 1 | |
| 02/12/2015 | 5 158.82 | 5 176.77 | 5 117.15 | 5 123.22 | 2 | |
| 03/12/2015 | 5 143.16 | 5 144.6 | 5 011.72 | 5 037.53 | 3 | |
| 04/12/2015 | 5 050.93 | 5 147 | 5 043.49 | 5 142.27 | 4 | |
| 07/12/2015 | 5 139.46 | 5 139.78 | 5 082.23 | 5 101.81 | 5 | 5 112.23 |
| 08/12/2015 | 5 050.52 | 5 111.73 | 5 045.73 | 5 098.24 | 6 | 5 107.57 |
| 09/12/2015 | 5 077.21 | 5 106.37 | 5 000.12 | 5 022.87 | 7 | 5 079.33 |
| 10/12/2015 | 5 026.3 | 5 075.65 | 5 019.31 | 5 045.17 | 8 | 5 067.95 |
| 11/12/2015 | 4 979.77 | 4 996.19 | 4 928.67 | 4 933.47 | 9 | 5 023.12 |
| 14/12/2015 | 4 932.61 | 4 953.6 | 4 871.59 | 4 952.23 | 10 | 4 999.49 |
| 15/12/2015 | 4 991.21 | 5 026.54 | 4 986.99 | 4 995.36 | 11 | 4 998.11 |
Vous pouvez télécharger cet exemple en format Excel
La figure-3 des cours journalier de l’indice allemand DAX avec deux moyennes mobile exponentielles de 20 jours et de 50 Jours.
Moyennes mobiles simples versus exponentielles
La différence de taille c’est que la moyenne mobile exponentielle réagit plus vite au dernier cours par rapport à la moyenne mobile simple qui est à la traine. Mais d’un autre côté la moyenne mobile simple comme elle est plus lisse, génère moins de faux signaux (whipsaws en anglais) par rapport à la moyenne mobile exponentielle qui réagit plus vite au derniers cours.
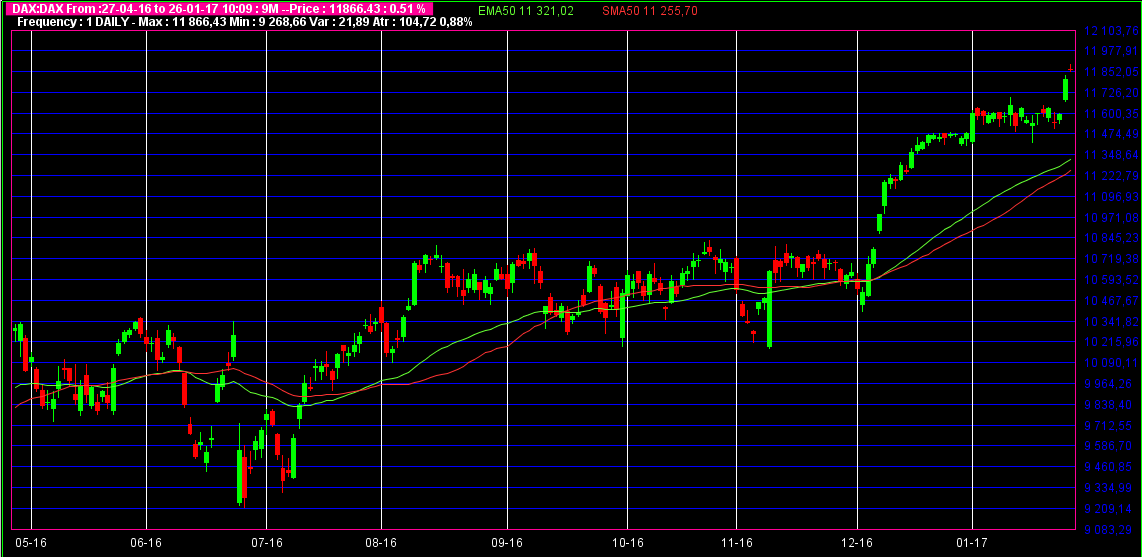
La figure-4 montre le DAX avec deux moyennes mobiles ; une simple de 50 jours et une exponentielle de 50 jours aussi. Ce qu’on constate, c’est que la moyenne mobile exponentielle réagit plus vite au changement des cours et elle est plus proche des cours de la moyenne mobile simple.
En conclusion, la moyenne mobile exponentielle est mieux adaptée pour des périodes courtes et la moyenne mobile simple est pour les périodes de long terme comme la 200
La prochaine publication concernera l’utilisation des moyennes mobiles
Laisser un commentaire